TLDR: I made a game of snake in which you control the snake by pointing your head. It uses your device’s camera and a pretrained TensorFlow model to estimate the direction your head is pointing in.
A week ago or so I decided to take on a hobby programming project. I wanted to make something involving machine learning that was somehow interactive, and I wanted it to run in the browser so that it could be hosted with GitHub pages to minimise worries about servers.
I knew that one of the clever things about TensorFlow is that it makes it relatively straightforward to run a trained model on various platforms, so I looked into TensorFlow.js as a way to run models in the browser.
As a first mini-project in this direction, I made a digit-classifier trained using MNIST. Here’s a demo:

You can see the live version here, and the code on GitHub here.
Training the model was nothing new to me, but having never properly learned JavaScript, there were many things that I had to learn by debugging. Here are a few things I learned about: drawing on a canvas; converting a canvas into a grid of pixels; asynchronous functions (I still don’t understand how to properly deal with promises and “thenable” objects to be honest); disabling pull-to-refresh.
Now armed with the knowledge of how to actually run TensorFlow models in the browser, I decided to make something slightly less trivial. While looking through the TensorFlow.js examples, I saw a demo of a model that estimates the geometry of faces from 2D images. I thought this was cool and wanted to make something with it!
The simplest non-trivial thing I could think of was to use the model to estimate the direction that the user’s head was pointing in — up, down, left, right or straight ahead. I had previously made a game of snake as a warm-up JavaScript exercise and thought it would be cool to be able to play by moving your head rather than using the keyboard to control the snake. Here’s a demo:
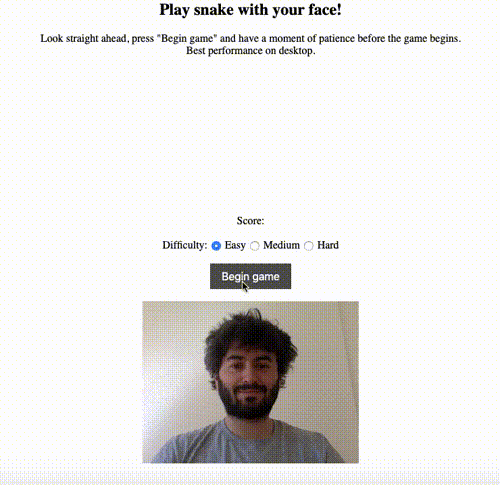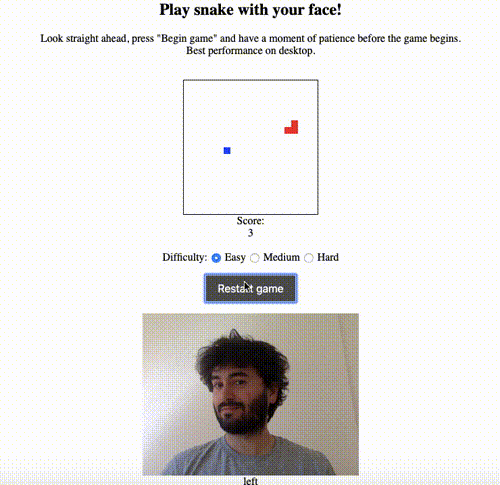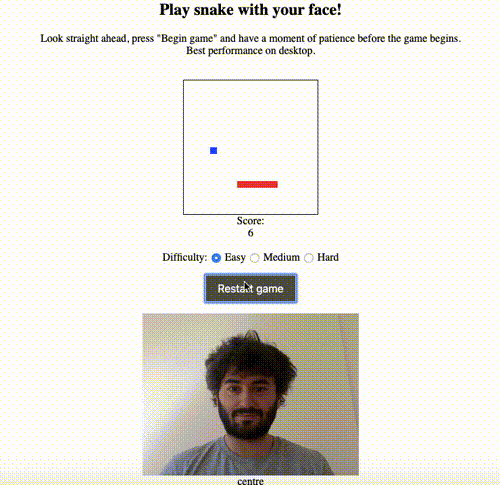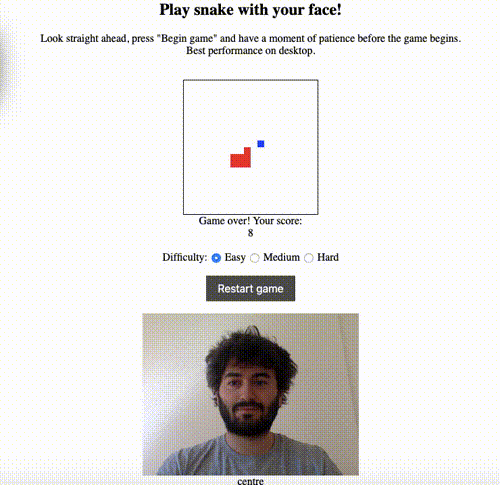
The live version is here, and the code is on GitHub here.
I’ll briefly explain in the rest of this post how the head-direction estimation works. (The actual snake part of this is just straightforward basic JavaScript, so I won’t discuss that here.)
The face mesh model from the TensorFlow.js examples accepts an image as input and outputs estimates of the 3-dimensional locations of ~400 facial landmarks. These points form the vertices of a mesh that describes the face. For instance, there are ~10 points determining the boundaries of the upper and lower lips and each eyelid. Although the model outputs locations for all of these landmarks, we only make use of a few.
The high level idea is to model the face as a flat plane, and to estimate the normal vector of this plane. That vector points in the direction that the face is looking. To find the normal vector of any plane, you can take any two non-parallel vectors lying in the plane and take their cross product.
Here, we locate the centre of the mouth by averaging the coordinates of the lip landmarks. We also locate the left and right cheeks, and consider the vectors lip -> left cheek and lip -> right cheek. The cross product gives us roughly the direction the face is pointing. (This is a 3D vector with x denoting left-right, y denoting up-down, and z denoting in/out of the screen.)
This is a very crude way to model the face, so if the vector we calculated has a positive y-component, it doesn’t necessarily mean that the user is actually looking up. So we introduce another heuristic to detect which direction the snake should move.
At the beginning of the game, the user is asked to look straight ahead, giving a reference vector. Subsequent estimated vectors are compared to this reference. If the y coordinate has increased/decreased by a sufficiently significant amount relative to the reference, the direction is classified as up/down respectively. Similarly, if the x coordinate has increased/decreased by a sufficiently significant amount relative to the reference, the direction is classified as left/right respectively. (In the case that both x and y coordinates changed significantly, the left/right direction takes precedence, and ‘sufficiently significant’ is a parameter that has to be chosen.)
It’s very crude, but because this is an interactive game, the user adapts to the algorithm, so we don’t have to worry too much to get something that works (of course, if this were part of a product we’d have to worry a lot more about everything working smoothly).
There are still several things to improve. First, it’s not as responsive as I’d like. I presume this is because it takes some time to execute the model and estimate the face landmark locations. Also, the refresh rate can’t be too high or my laptop fan starts to whirr. Clearly it should be possible to improve on this, since we aren’t using almost all of the information output by the model being used! Second, it doesn’t work great on mobile, I presume because of the less powerful computational resources available. It would be great to dive into using the specialised hardware on some new phones (e.g. The newest Pixel’s Neural Core and the iPhone’s Bionic chip), but that’s a project for another day.